引言

在数学的世界中，函数是描述事物变化规律的强大工具。函数的斜率，即导数，反映了函数变化的速率。本文将探讨一类斜率不断减小的常见函数，这类函数在数学分析、物理学和经济学等领域有着广泛的应用。

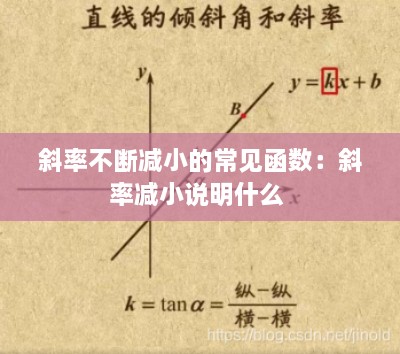
斜率的概念

函数的斜率，即导数，是函数在某一点处的变化率。对于一元函数$f(x)$，其在$x_0$点的导数表示为$f'(x_0)$，它描述了当$x$从$x_0$微小增加时，$f(x)$的增量与$x$的增量之比。如果导数$f'(x)$在某个区间内始终小于零，则说明函数在该区间内是单调递减的。

斜率不断减小的函数类型

斜率不断减小的函数通常具有以下特点：

• 导数始终为负值。
• 函数图像呈现出向下倾斜的趋势。
• 随着自变量的增加，函数值的增长速度逐渐减缓。

以下是一些常见的斜率不断减小的函数类型：

指数衰减函数

指数衰减函数是斜率不断减小的典型代表。这类函数通常具有以下形式：$f(x) = a \cdot e^{kx}$，其中$a$和$k$是常数。指数衰减函数的导数为$f'(x) = k \cdot a \cdot e^{kx}$。由于$k$是负值，所以导数始终小于零，使得函数图像呈现下降趋势。常见的指数衰减函数包括放射性衰变模型和人口衰减模型。

对数函数的倒数

对数函数的倒数也是一类斜率不断减小的函数。例如，函数$f(x) = \frac{1}{\ln(x)}$，其中$\ln(x)$是自然对数。对数函数的导数为$f'(x) = -\frac{1}{x(\ln(x))^2}$。由于$\ln(x)$在$(0, +\infty)$区间内始终大于零，所以导数始终小于零。这种函数在经济学和物理学中有着广泛的应用，如人口增长和物质衰减等。

多项式函数

多项式函数中，高次项的系数为负值时，其导数也将不断减小。例如，函数$f(x) = -x^3 + 2x^2 - 5$的导数为$f'(x) = -3x^2 + 4x$。随着$x$的增加，导数的绝对值逐渐减小，表明函数的斜率在不断减小。这类函数在物理学和工程学中有着广泛的应用，如力学和电路分析等。

应用实例

斜率不断减小的函数在多个领域都有实际应用：

• 物理学：描述物体的衰减过程，如放射性物质的衰变、热量的散失等。
• 经济学：分析市场的供需关系，如产品销售量随时间的变化、消费者对价格的敏感度等。
• 生物学：研究生物种群的增长与衰减，如传染病传播、物种灭绝等。

这些函数的斜率不断减小，反映了事物发展的规律，有助于我们更好地理解现实世界中的各种现象。

结论

斜率不断减小的函数在数学分析和实际问题中都有着重要的地位。通过了解这些函数的特性，我们可以更好地把握事物发展的趋势，为科学研究、工程设计和经济决策提供有力支持。本文对指数衰减函数、对数函数的倒数和多项式函数等常见斜率不断减小的函数进行了简要介绍，希望对读者有所帮助。